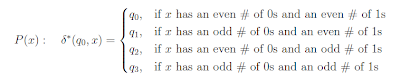Stay with me and watch me chronicle my learning over the next week and a half as I prepare for an out-of-the-blue front end job interview.
This is the path we'll take:
http://blog.sourcing.io/interview-questions
https://github.com/darcyclarke/Front-end-Developer-Interview-Questions
http://stackoverflow.com/questions/2863435/front-end-developer-interview-questions
http://css-tricks.com/interviewing-front-end-engineer-san-francisco/
http://darcyclarke.me/development/front-end-job-interview-questions/
http://engineering.appfolio.com/2012/11/16/css-architecture/
maybe not in that order, though.
Here we go!
dark roast and pumpkin, please.
Thursday 13 March 2014
Thursday 29 November 2012
Really stumped
How does this happen:
so I don't understand how they got from
δ (q1, 0) if x odd 0 even 1
δ (q2, 0) if x even 0 odd 1
δ (q3, 0) if x odd 0 odd 1
(δ (q0, 0) = q1 if x even 0 even 1 makes sense)
_______________________________________________
_______________________________________________
Got it.
Look directly at the diagram, and do the step.
Is that mathematically rigorous, though?
provided the transition function is defined like this:
???
It seems the transition function is only defined for a start state of q0.
so I don't understand how they got from
δ (q1, 0) if x odd 0 even 1
δ (q2, 0) if x even 0 odd 1
δ (q3, 0) if x odd 0 odd 1
(δ (q0, 0) = q1 if x even 0 even 1 makes sense)
_______________________________________________
_______________________________________________
Got it.
Look directly at the diagram, and do the step.
Is that mathematically rigorous, though?
Workthrough Thoughts
on p. 193
"Note that a language may be an infinite set; each string in the language, however, is finite."
Question:
Can you have a set that supports infinite strings? Not an infinite number of strings, but strings that are themselves infinite?
Is a string of infinite length even a reasonable concept to propose?
If a "length" is infinite, can it even reasonably be said to be a "length"? ... more like a lack of length?
(More musings: Maybe "lack of length" is reserved for the empty string, which has no length? Though I suppose a length of 0 is indeed a length. Just a 0 length.)
-----------------------------
I know that x^2 >= 2x so long as x >= 2, we've proved that.
But now to show that x^2 > = 2x - 1 so long as x > = 0 ?
-----
Got it!
x^2 >= 2x is stronger than x^2 > = 2x - 1
So x^2 >= 2x -1 is already true for all x >= 2.
The only additional cases you need to consider to get from true for all x >= 2 to true for all x>= 0 are 0 and 1. These can be shown directly.
"Note that a language may be an infinite set; each string in the language, however, is finite."
Question:
Can you have a set that supports infinite strings? Not an infinite number of strings, but strings that are themselves infinite?
Is a string of infinite length even a reasonable concept to propose?
If a "length" is infinite, can it even reasonably be said to be a "length"? ... more like a lack of length?
(More musings: Maybe "lack of length" is reserved for the empty string, which has no length? Though I suppose a length of 0 is indeed a length. Just a 0 length.)
-----------------------------
I know that x^2 >= 2x so long as x >= 2, we've proved that.
But now to show that x^2 > = 2x - 1 so long as x > = 0 ?
-----
Got it!
x^2 >= 2x is stronger than x^2 > = 2x - 1
So x^2 >= 2x -1 is already true for all x >= 2.
The only additional cases you need to consider to get from true for all x >= 2 to true for all x>= 0 are 0 and 1. These can be shown directly.
Wednesday 28 November 2012
Proving recursive algorithms
Reading through the remainder of Chapter 2 (2.7 onward) in attempts to answer my below question, I wonder why the examples use an array of length 1 as the base case instead of an array of length 0.
Then I get to this:
and now I am puzzled. That is not all the cases? a subarray of length 0 is definitely still a subarray. Hopefully reading on will solve the mystery, else I'll have to work through it on my own.
------------------------------
Got it. Well, half of it.
The precondition was that A is a non-empty array. So I suppose that's why the base case is an array of length 1?
Still mediumly confused though because an array of length 1 can have a subarray of length 0.
--------------------------
I suppose a "correctness specification" is the recursive analogue of an iterative loop invairant?
-------------------------
Aside : Can you have an array of infinite length?!
Motivation:
It seems that for termination it suffices to show that a recursive call operates on a smaller section of the array each time. But if the array was infinitely long, would that actually make it end?
First Thought:
But we have the theorem that all decreasing sequences of Natural numbers are finite, so does that mean that smaller and smaller sections of the array must eventually culminate in a subarray of size 0 ? (or of size 1 if we're adhering to the strange base case specifications above?).
Is a countdown from infinity still a veritable countdown?
Does this theorem hold if there's no defined start of the sequence?
------------------------------
Then I get to this:
and now I am puzzled. That is not all the cases? a subarray of length 0 is definitely still a subarray. Hopefully reading on will solve the mystery, else I'll have to work through it on my own.
------------------------------
Got it. Well, half of it.
The precondition was that A is a non-empty array. So I suppose that's why the base case is an array of length 1?
Still mediumly confused though because an array of length 1 can have a subarray of length 0.
--------------------------
I suppose a "correctness specification" is the recursive analogue of an iterative loop invairant?
-------------------------
Aside : Can you have an array of infinite length?!
Motivation:
It seems that for termination it suffices to show that a recursive call operates on a smaller section of the array each time. But if the array was infinitely long, would that actually make it end?
First Thought:
But we have the theorem that all decreasing sequences of Natural numbers are finite, so does that mean that smaller and smaller sections of the array must eventually culminate in a subarray of size 0 ? (or of size 1 if we're adhering to the strange base case specifications above?).
Is a countdown from infinity still a veritable countdown?
Does this theorem hold if there's no defined start of the sequence?
------------------------------
dos cosas
uno:
The previous post was incorrect. The loop invariant did not, in fact, remain unchanged. Though the loop invariant as it were was correct, it was not helpful in proving the post condition. I struggled to derive what would be the new invariant, but after excessive trial and error I realized that I was going to have to rely on the loop invariant to prove the postcondition, so looking at the postcondition should have been my first step in trying to determine one.
and so I did!
which leads me to.....
dos:
I SUCCESSFULLY PROVED MY FIRST PROGRAM.
yeyeyeyeyeye
Virtual high fives all around. (y)
The previous post was incorrect. The loop invariant did not, in fact, remain unchanged. Though the loop invariant as it were was correct, it was not helpful in proving the post condition. I struggled to derive what would be the new invariant, but after excessive trial and error I realized that I was going to have to rely on the loop invariant to prove the postcondition, so looking at the postcondition should have been my first step in trying to determine one.
and so I did!
which leads me to.....
dos:
I SUCCESSFULLY PROVED MY FIRST PROGRAM.
yeyeyeyeyeye
Virtual high fives all around. (y)
Subscribe to:
Posts (Atom)